Geometry
MagTense Parameters
integer :: tileType
real :: r0, theta0, z0, dr, dtheta, dz
real :: a, b, c
real,dimension(3,4) :: vert
real,dimension(3) :: offset
real,dimension(3) :: rotAngles
With the mentioned parameters a tile can be arbitrarily defined in the global coordinate system. For each tile an individual local coordinate system is created.
Tile Types
1 = cylindrical tile
2 = prism
3 = circular piece
4 = inverted circular piece
5 = tetrahedron
6 = sphere
7 = spheroid
Offset
The offset is a three-dimensional vector, which determines the difference between the origin of the global coordinate system to the local coordinate system.
Rotation Angles
The rotation angles [radians] define the rotation of a tile in its local coordinate system. A tile can be rotated around its local axis with yaw (rotation around local z-axis, \(\psi\)), pitch (rotation around local y-axis, \(\theta\)) and roll (rotation around local x-axis, \(\phi\)).
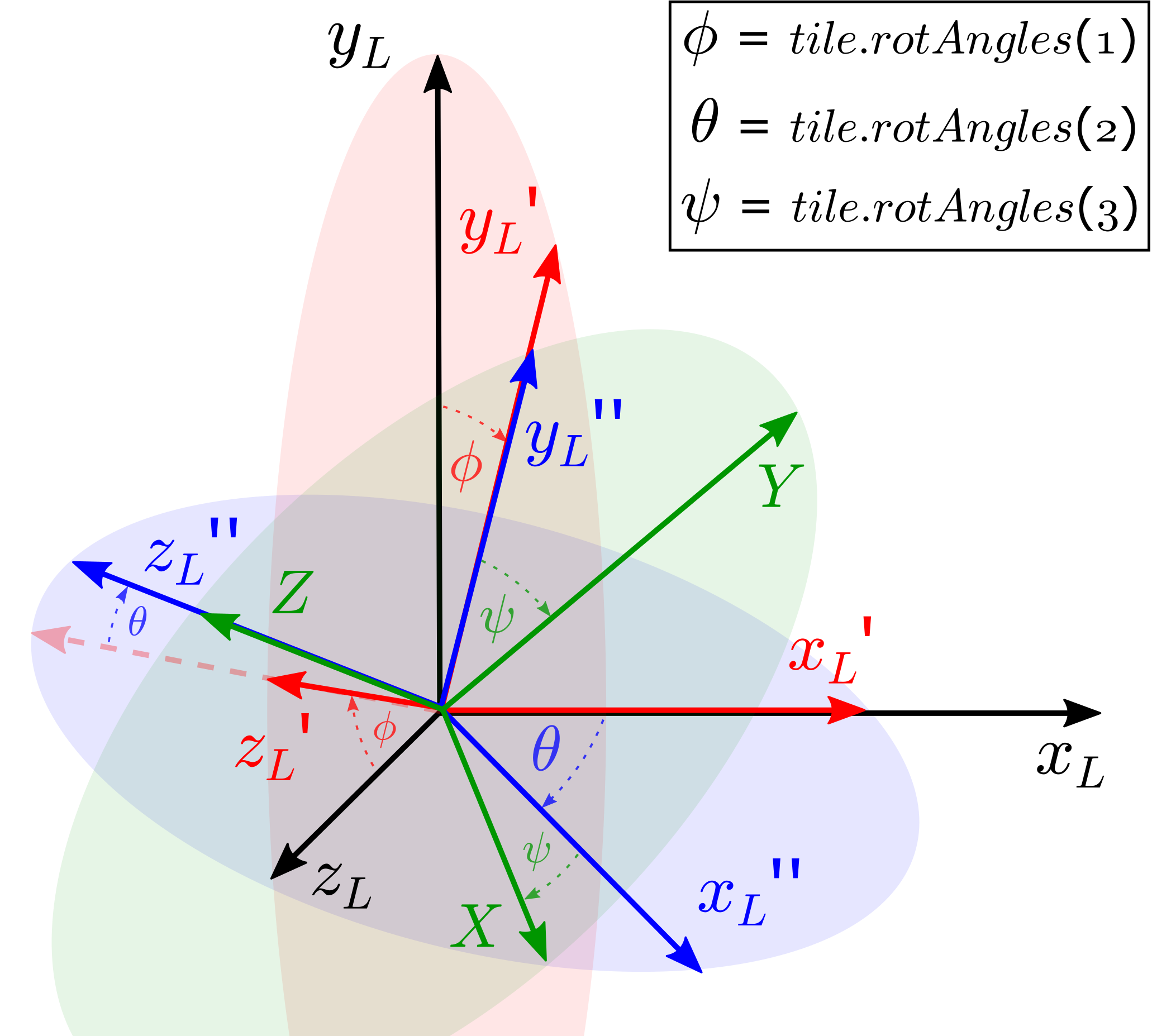
Rotations of a tile are performed in its local coordinate system. Firstly, the tile is rotated with \(\phi\) around its local x-axis. Secondly, the local y-axis is rotated by \(\theta\). Eventually, the angle \(\psi\) is performed around the local z-axis.
Set geometric dimensions
Cylindrical Tile
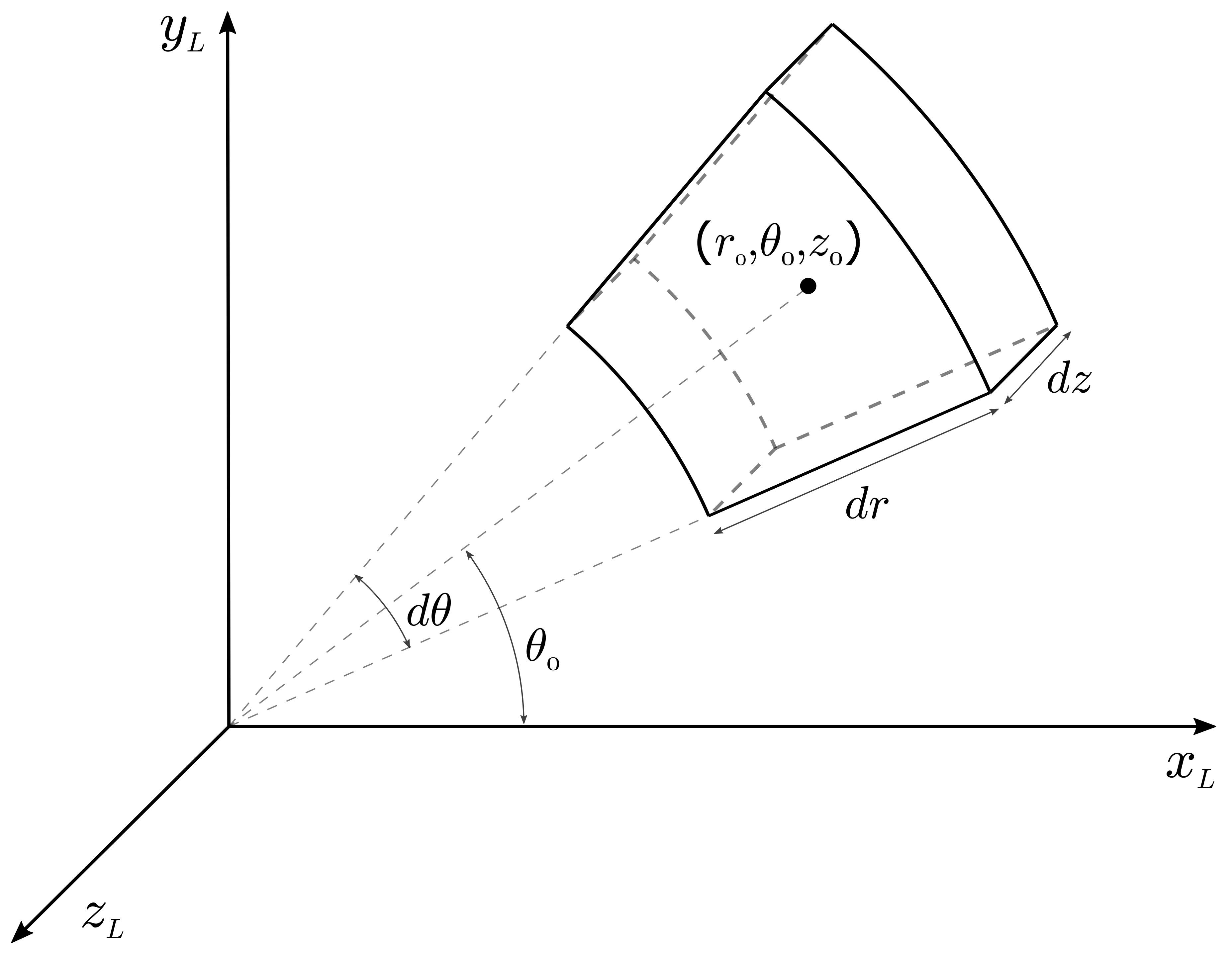
The cylindrical tile is defined in cylindrical coordinates with respect to its local coordinate system. The center point is located at \((r_0, \theta_0, z_0)\). The extensions in each direction are given with \(dr, d\theta\) and \(dz\), respectively.
Examples of how to compute the magnetic field from such a tile are given in Matlab and python.
Prism
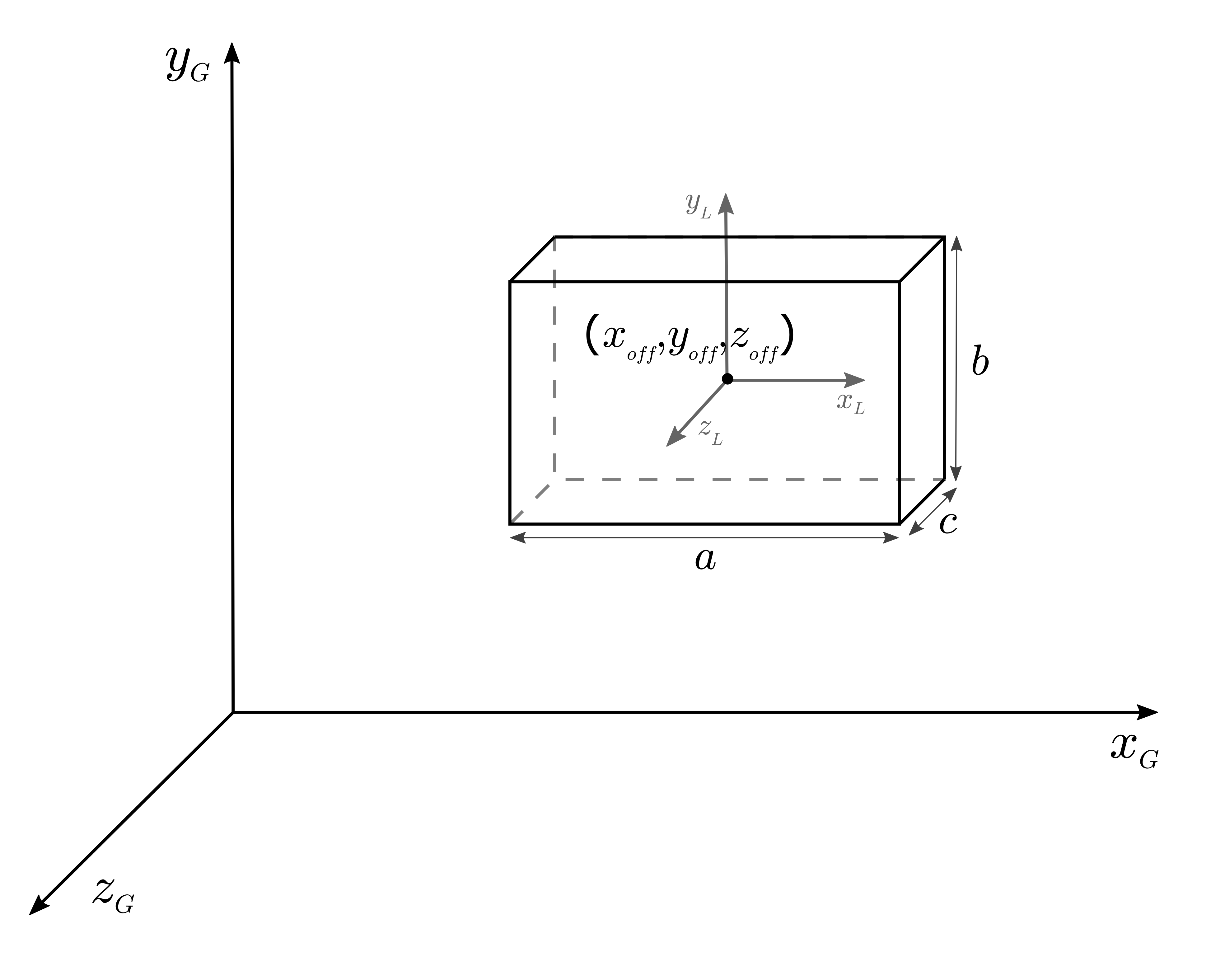
The prism is defined by the side lengths \(a, b\) and \(c\). Its center coordinate is \((x_{off}, y_{off}, z_{off})\) in the global coordinate system.
Examples of how to compute the magnetic field from such a tile are given in Matlab and python.
Circular Piece

The circular piece is defined by its center point (\(r_0, \theta_0, z_0\)) in the local coordinate system. The midpoint of the outer circular edge is given with a translation of \(\frac{dr}{2}\) from the center point. The extensions in the others directions are given with \(d\theta\) and \(dz\). In contrast to the cylindrial tile, the inner edges are parallel to the local x-axis and y-axis and from a right angle.
Examples of how to compute the magnetic field from such a tile are given in python.
Inverted Circular Piece
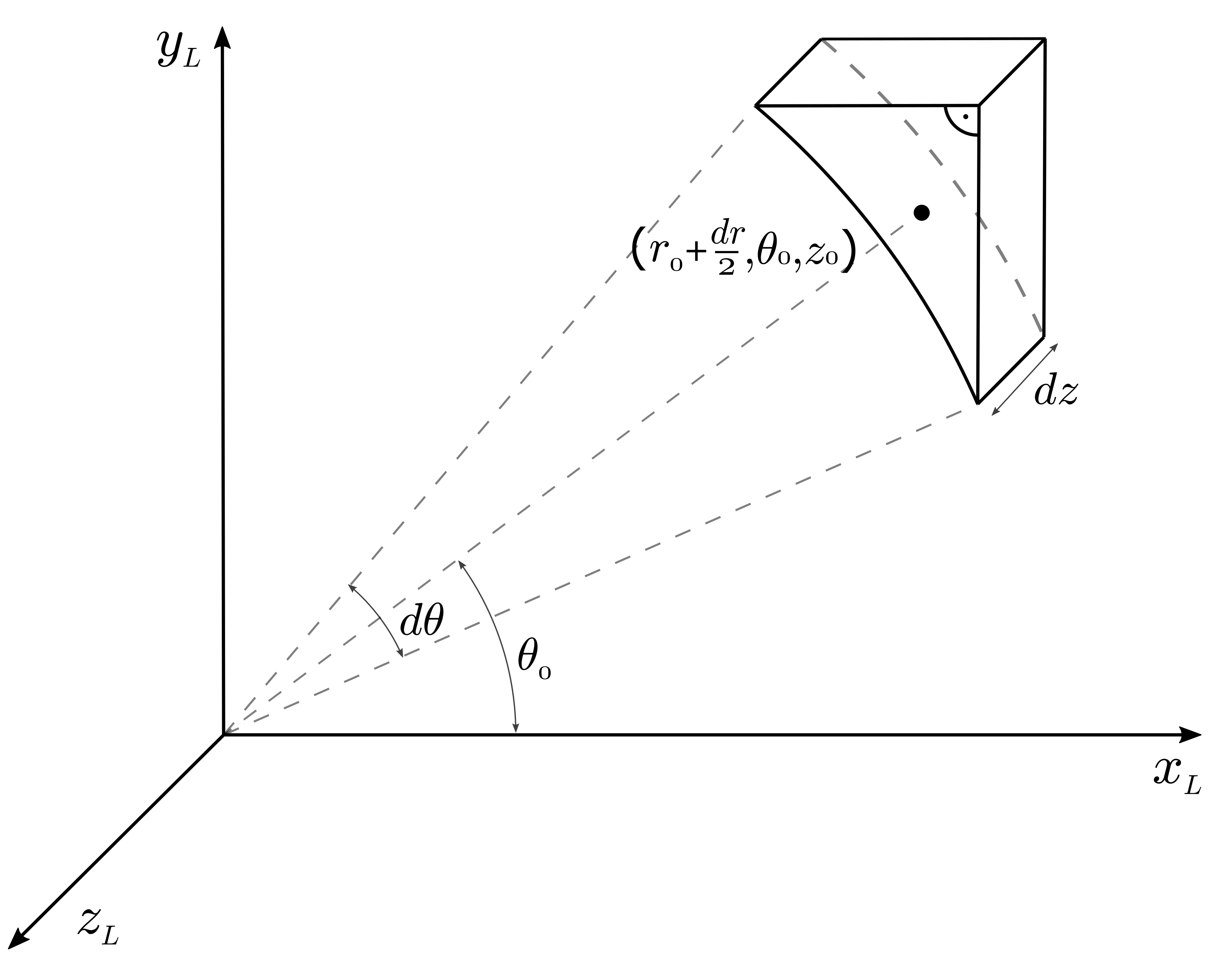
The midpoint of the inner circular edge is located at (\(r_0 + \frac{dr}{2}, \theta_0, z_0\)) in the local coordinate system. The angular extension in each direction is \(\frac{d\theta}{2}\) extensions and the height of such a tile is \(dz\). The outer edges are parallel to the local x-axis and y-axis and from a right angle. Therefore, its naming is “inverted circular piece”.
Examples of how to compute the magnetic field from such a tile are given in python.
Tetrahedron
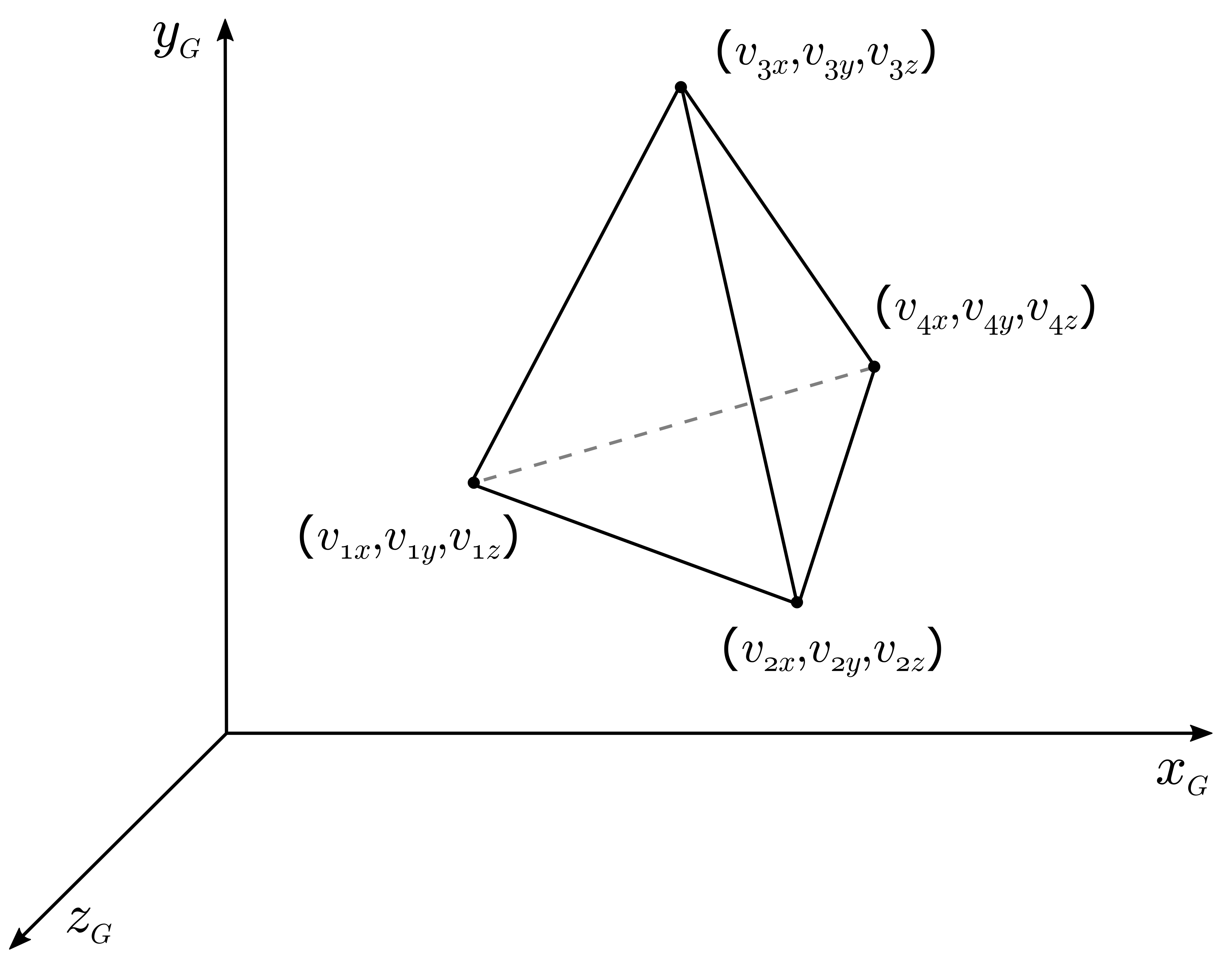
A tetrahedron is specified by its four vertices in the global coordinate system.
Examples of how to compute the magnetic field from such a tile are given in Matlab and python.
Sphere
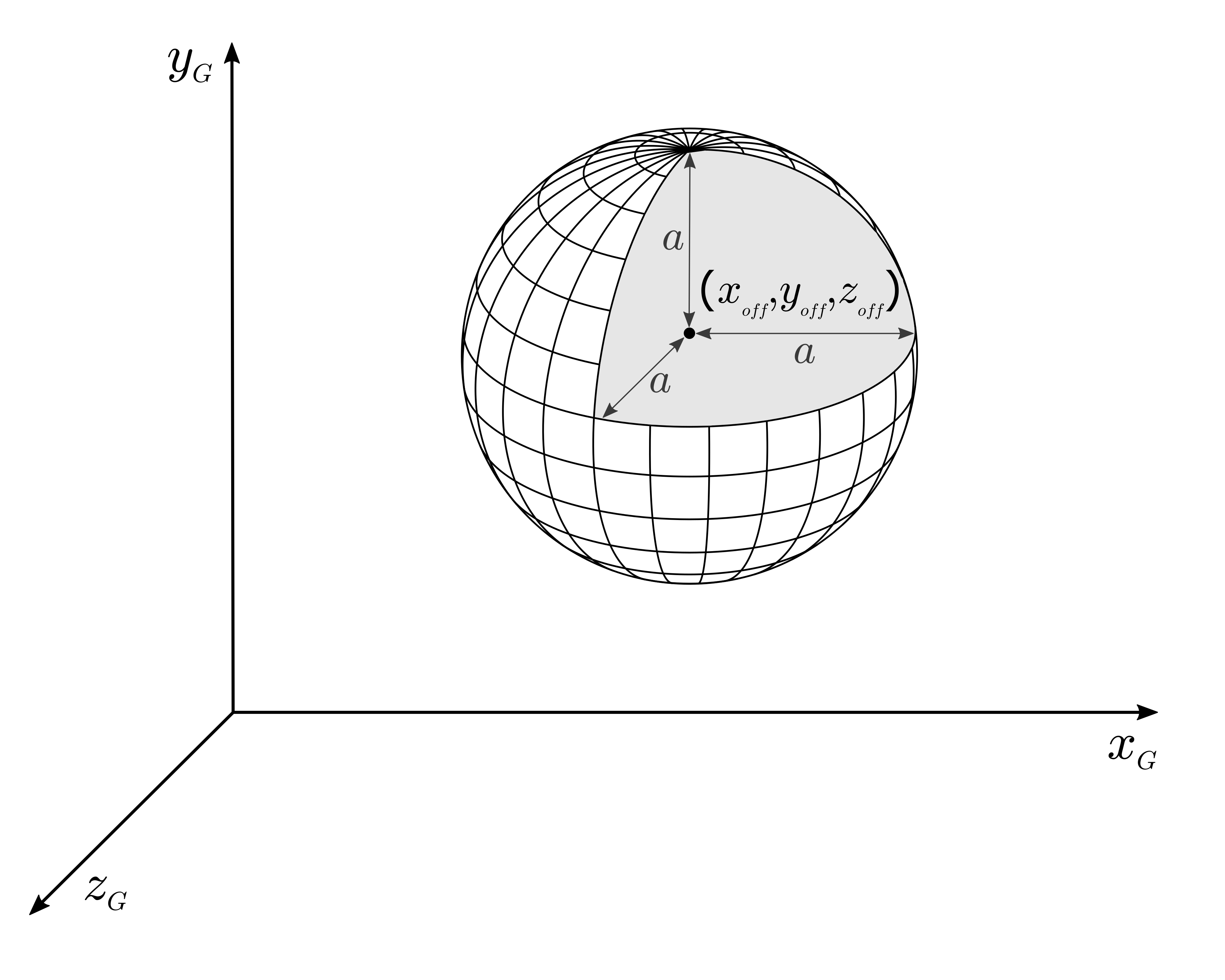
A sphere is fully defined by its radius \(a\). Its center coordinate is \((x_{off}, y_{off}, z_{off})\) in the global coordinate system.
Examples of how to compute the magnetic field from such a tile are given in Matlab and python.
Spheroid

Its center coordinate is \((x_{off}, y_{off}, z_{off})\) in the
global coordinate system.
The axial radii can be specified with \(a, b\) and \(c\),
whereas two radii must have the same length.
If \(b < a\), then we have a oblate spheroid.
If \(b > a\), then a prolate spheroid is constructed.
In praxis, any of the axial radii can be chosen to differ from the others.
As a specialty of this geometry, rotation may be also defined as a rotation axis pointing in a given direction. One can either choose the symmetry axis (axis with a radius different to the other ones) or the c-axis. The arguments are defined in the interfaces and are translated to the corresponding rotation angles in the local coordinate system.
Examples of how to compute the magnetic field from such a tile are given in Matlab and python.